The Q-Q (Quantile-Quantile) Plot helps you assess whether your data follows a normal distribution by comparing your sample quantiles against theoretical normal quantiles. Combined with the Shapiro-Wilk normality test, it provides both visual and statistical evidence of normality. It's particularly useful for validating assumptions in statistical tests, analyzing regression residuals, and identifying potential outliers. Simply input your data to create an Q-Q plot and calculate the corresponding Shapiro-Wilk test statistics. You can test this plot maker by loading the sample dataset named "tips" and select the "total_bill" column.
If you need more comprehensive normality testing, consider using the Normality Test Calculator, which performs three different normality tests (Shapiro-Wilk, Anderson-Darling, and Kolmogorov-Smirnov) and provides detailed results and visualizations.
Calculator
1. Load Your Data
2. Select Columns & Options
💡 With "None" selected, you can customize the chart
Related Calculators
Learn More
What is a Q-Q Plot?
A Q-Q (Quantile-Quantile) plot is a graphical tool used to assess whether a dataset follows a normal distribution. It plots the quantiles of your data against the theoretical quantiles of a normal distribution, creating a visual way to identify departures from normality.
How to Interpret Q-Q Plots
Normal Data Patterns
- Points follow the diagonal reference line closely
- Minor random deviations are acceptable
- No systematic curves or patterns
- Points near center of line often fit better than extremes
Common Deviations
- S-shaped curve: Indicates skewness
- Points above line at ends: Heavy tails
- Points below line at ends: Light tails
- Outliers: Points far from line at either end
Pattern Recognition Guide
Understanding specific patterns in your QQ plot helps diagnose exactly how your data deviates from normality:
S-Shaped Curves (Skewness)
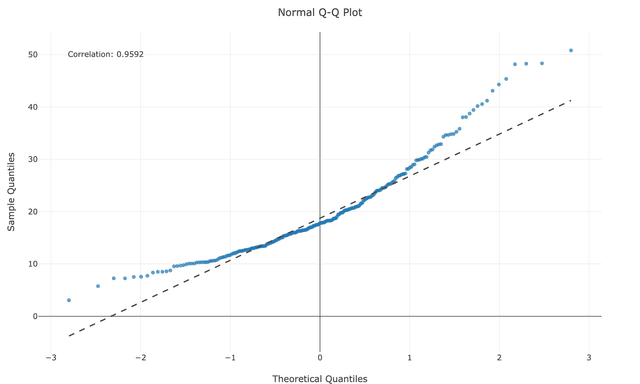
- Concave upward: Points curve above line in lower part, below in middle, above in upper part
- Interpretation: Positive skewness (right-tailed distribution)
- Example causes: Income data, reaction times, many biological measurements
Reversed S-Curves

- Concave downward: Points curve below line in lower part, above in middle, below in upper part
- Interpretation: Negative skewness (left-tailed distribution)
- Example causes: Age at death data, exam scores with ceiling effects
Kurtosis Patterns
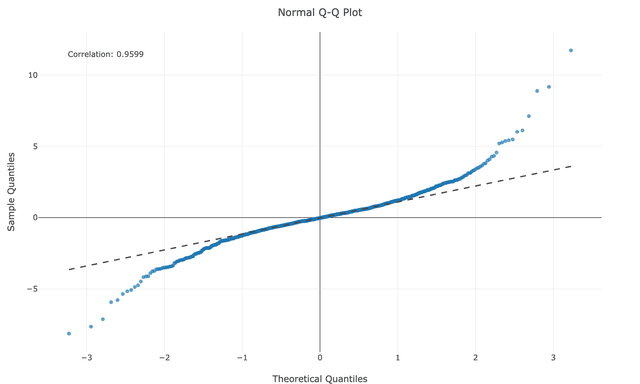
- Both tails above line: Heavy tails (leptokurtic) - more extreme values than normal
- Both tails below line: Light tails (platykurtic) - fewer extreme values than normal
- Example causes: Financial returns (heavy), bounded measurements (light)
Outlier Patterns
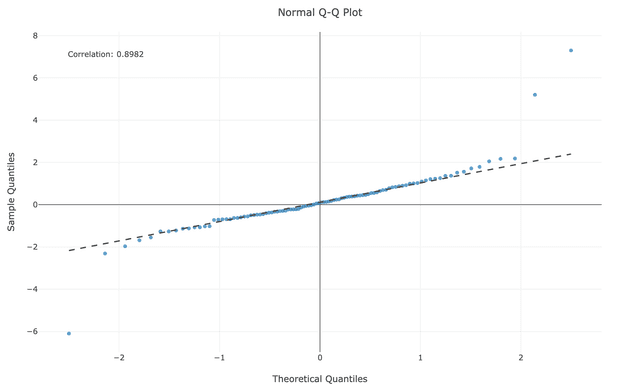
- Most points follow line but a few points at ends sharply deviate
- Interpretation: Potential outliers rather than distribution issues
- Action: Investigate individual points for measurement errors or special cases
Pro Tip
Transformation Methods
When your data isn't normally distributed, transformations can help normalize it for statistical analysis:
For Positive Skewness (Right-Skewed Data)
Log Transformation
new_value = log(original_value)
Best for: Highly skewed data that spans multiple orders of magnitude. Common in finance, biology, and economics. Requires all values to be positive.
Square Root Transformation
new_value = sqrt(original_value)
Best for: Moderately skewed data or count data that follows a Poisson distribution. Requires non-negative values.
Reciprocal Transformation
new_value = 1/original_value
Best for: Very highly skewed data. Note that this reverses the order of values.
For Negative Skewness (Left-Skewed Data)
Square Transformation
new_value = original_value²
Best for: Mildly to moderately left-skewed data.
Cube Transformation
new_value = original_value³
Best for: More severely left-skewed data.
Reflect and Log Transform
new_value = log(max_value + 1 - original_value)
Best for: Severe negative skewness. This approach reflects the distribution, applies a log transform, then can be reflected back if needed.
Advanced Transformation Methods
Box-Cox Transformation
new_value = (original_value^λ - 1)/λ for λ ≠ 0,
new_value = log(original_value) for λ = 0
Best for: Finding the optimal transformation by automatically selecting the lambda parameter that best normalizes the data. Requires positive values.
Yeo-Johnson Transformation
Similar to Box-Cox but works with negative values as well.
Best for: When you need a Box-Cox-like approach but have negative values in your dataset.
Robust Scaling
new_value = (original_value - median) / IQR
Best for: When outliers are distorting your distribution. This uses the median and interquartile range instead of mean and standard deviation.
Important Note
Try Our Transformation Tool
Ready to transform your data? Our Normality Transformation Tool lets you apply log, square, and Box-Cox transformations with just a few clicks.
Creating Q-Q Plots in R
R provides excellent tools for creating Q-Q plots. Here's a simple example using ggplot2:
library(tidyverse)
# Load sample dataset
tips <- read.csv("https://raw.githubusercontent.com/plotly/datasets/master/tips.csv")
# Create Q-Q plot
ggplot(tips, aes(sample = total_bill)) +
stat_qq() +
stat_qq_line(color = "red") +
labs(title = "Normal Q-Q Plot for Total Bill",
x = "Theoretical Quantiles",
y = "Sample Quantiles") +
theme_minimal()
This code creates a Q-Q plot for the 'total_bill' variable from a restaurant tips dataset. The red line represents the theoretical normal distribution.
Creating Q-Q Plots in Python
Python also provides powerful libraries for creating Q-Q plots. Here's an example using Matplotlib and SciPy:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import seaborn as sns
tips = pd.read_csv("https://raw.githubusercontent.com/plotly/datasets/master/tips.csv")
fig, ax = plt.subplots(figsize=(8, 6))
stats.probplot(tips['total_bill'], dist="norm", plot=ax)
ax.set_title("Normal Q-Q Plot for Total Bill", fontsize=14, fontweight='bold')
ax.set_xlabel("Theoretical Quantiles", fontsize=12)
ax.set_ylabel("Sample Quantiles", fontsize=12)
ax.grid(True, alpha=0.3)
line = ax.get_lines()[1]
line.set_color('red')
line.set_linewidth(2)
plt.tight_layout()
plt.show()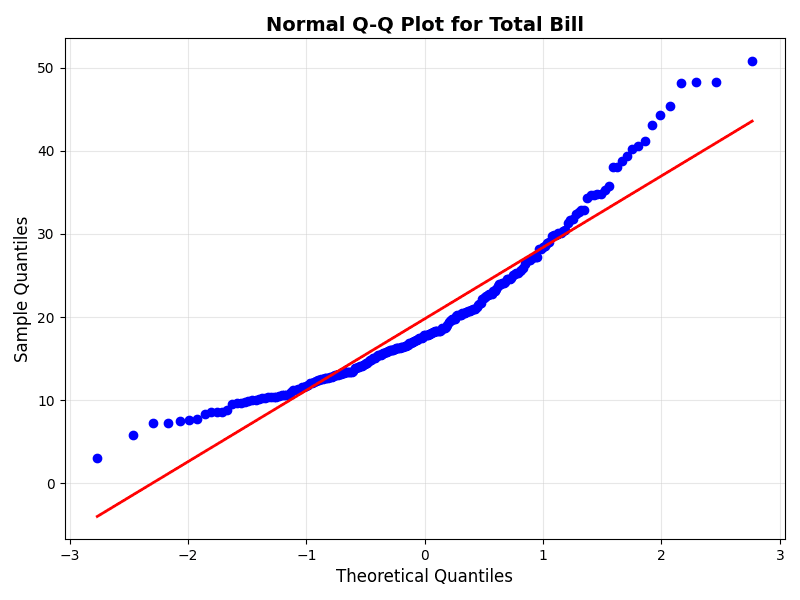
Alternatively, you can use the Seaborn library for a easier approach with built-in styling:
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
import seaborn as sns
tips = pd.read_csv("https://raw.githubusercontent.com/plotly/datasets/master/tips.csv")
plt.figure(figsize=(8, 6))
sns.set_style("whitegrid")
# Create Q-Q plot with seaborn styling
stats.probplot(tips['total_bill'], dist="norm", plot=plt)
plt.title("Normal Q-Q Plot for Total Bill")
plt.show()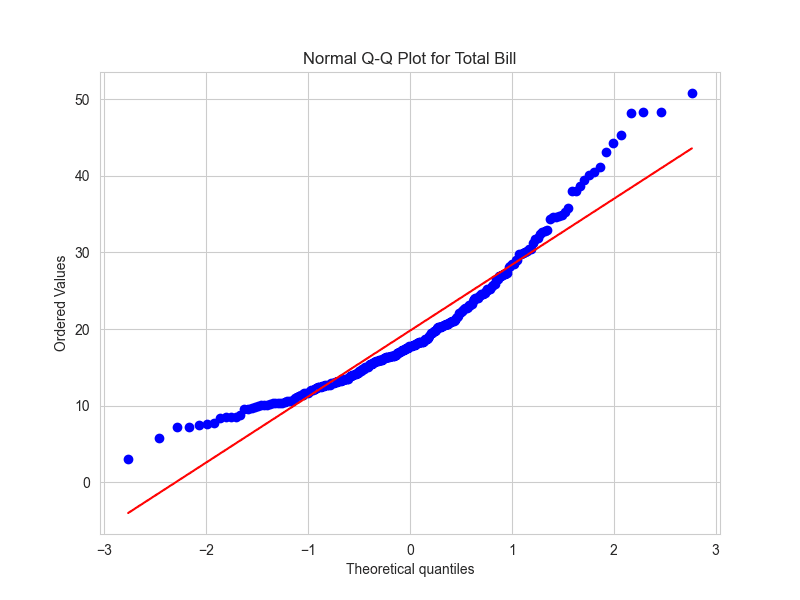
When to Use Q-Q Plots
Q-Q plots are particularly useful in these situations:
- Checking assumptions for statistical tests (t-tests, ANOVA, etc.)
- Validating normality of regression residuals
- Assessing the distribution of continuous variables
- Identifying potential outliers and their impact
Sample Size Considerations
The effectiveness of Q-Q plots and normality tests can vary with sample size:
- Small samples (n < 30): May not show clear patterns, harder to detect non-normality
- Medium samples (30-1000): Ideal range for both visual and statistical assessment
- Large samples (n > 1000): May show significant deviations even for approximately normal data
Making Decisions
When assessing normality, consider both the Q-Q plot and Shapiro-Wilk test results:
- If both show normality: Proceed with normal-theory statistics
- If both show non-normality: Consider transformations or non-parametric methods
- If results conflict: Examine sample size and consider practical significance of deviations
- For large samples: Give more weight to visual assessment than test p-values